试题 A: 九进制转十进制(5分)
问题描述
- 九进制正整数$(2022)_9$转换成十进制等于多少?
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可.本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分.
答案 :1478
思路
模拟,考察进制转换,$res= 2 \times 9^0 + 2 \times 9^1 + 0 \times 9^2 + 2 \times 9^3 =2+18+2 \times 729 = 1478$
代码
# 由于作者懒得写c++,直接上python代码
print(2*pow(9,0)+2*pow(9,1)+0*pow(9,2)+2*pow(9,3))
试题 B: 顺子日期(5分)
问题描述
- 小明特别喜欢顺子.顺子指的就是连续的三个数字:$123、456$等.顺子日期指的就是在日期的$yyyymmdd$表示法中,存在任意连续的三位数是一个顺子的日期.例如$20220123$就是一个顺子日期,因为它出现了一个顺子:$123$, 而$20221023$则不是一个顺子日期,它一个顺子也没有.小明想知道在整个$2022$年份中,一共有多少个顺子日期.
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可.本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分.
答案 存在争议 14 或 4
思路
枚举$2022$每一天检查其中是否存在连续的三个数字,由于告知$20221023$不是顺子日期,故逆序可能是不算是顺子日期,但是题目中未告知类似$012$算作顺子.
这难道是蠢蠢牛马地考语文阅读理解,我交的答案是$14$(已经开摆了,o(*≧д≦)o!!).
忽略前四位$2022$后(因为月份不可能以$3x$开头),故只考虑后四位有以下四大种情况(总共$14$种):
- $012x$,$x$的取值为$(0$~$9)$,共$10$种;
- $1012$,共$1$种;
- $1123$,共$1$种;
- $123y$,$y$的取值为$(0或1)$,共$2$种.
如果不算$012$的这种顺子,(忽略前四位)结果为:$0123$,$1123$,$1230$,$1231$.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
int res,days[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
int check(int temp)
{
int year=temp/10000;
int month=temp/100%100;
int day=temp%100;
if(month==0||month>=13)
return 0;
if(day>days[month])
return 0;
return 1;
}
int main()
{
for(int i=20220101;i<=20221231;i++)
if(check(i))
{
string s=to_string(i);
for(int j=0;j<=5;j++)
if(s[j+1]==s[j]+1&&s[j+2]==s[j]+2/*&&s[j]!='0'*/)
{//把注释部分加上考虑012不为顺子
res++;
cout << i << endl;
break;
}
}
cout << res << endl;
return 0;
}
试题 C: 刷题统计(10分)
问题描述
- 小明决定从下周一开始努力刷题准备蓝桥杯竞赛.他计划周一至周五每天做$a$道题目,周六和周日每天做$b$道题目.请你帮小明计算,按照计划他将在第几天实现做题数大于等于$n$题?
输入格式
输入一行包含三个整数$a$,$b$和$n$.
输出格式
输出一个整数代表天数.
输入样例
$10$ $20$ $99$
输出样例
$8$
评测用例规模与约定
- 对于$50$% 的评测用例,$1 \leqslant a, b, n \leqslant 10^6$.
- 对于$100$% 的评测用例,$1 \leqslant a, b, n \leqslant 10^{18}$.
思路
$10^{18}$的数据暴力肯定不行,需将所有的题对一周的总题数作除法,剩下的余数部分可通过枚举的方式解决,结果为$\frac{n}{5\times a + 2 \times b} \times 7+n$%$(5\times a + 2 \times b)$题数所需要花费的天数.
代码
//蓝桥杯中交的代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
ll a,b,n;
int main()
{
cin >> a >> b >> n;
ll sum=5*a+2*b;
ll res1=n%sum,res=n/sum*7;
if(res1<=5*a)
{
if(res1%a!=0)
res+=res1/a+1;
else res+=res1/a;
}
else
{
res+=5;
res1%=5*a;
if(res1%b!=0)
res+=res1/b+1;
else res+=res1/b;
}
cout << res << endl;
}
//y总的代码(稍微改了一下)
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
ll a,b,n;
int main()
{
cin >> a >> b >> n;
ll sum=5*a+2*b;
ll res=n/sum*7;
n%=sum;
ll d[8]={0,a,a,a,a,a,b,b};
for(int i=1;i<=7;i++)
{
if(n<=0)
break;
n-=d[i];
res++;
}
cout << res << endl;
return 0;
}
试题 D: 修剪灌木(10分)
问题描述
- 爱丽丝要完成一项修剪灌木的工作.
- 有$N$棵灌木整齐的从左到右排成一排.爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为$0$厘米,爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木.当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木.直到修剪了最左的灌木后再次调转方向.然后如此循环往复.
- 灌木每天从早上到傍晚会长高$1$厘米,而其余时间不会长高.在第一天的早晨,所有灌木的高度都是$0$厘米.爱丽丝想知道每棵灌木最高长到多高.
输入格式
一个正整数$N$,含义如题面所述.
输出格式
输出$N$行,每行一个整数,第$i$行表示从左到右第$i$棵树最高能长到多高.
样例输入
$3$
样例输出
$4$
$2$
$4$评测用例规模与约定
- 对于$30$% 的评测用例,$N \leqslant 10$.
- 对于$100$% 的评测用例,$1 < N \leqslant 10000$.
思路
找规律(或模拟),反正我是暴力模拟t了,其实模拟也能过,忘了测大数据了,tcl,我的代码就不给了. U•ェ•*U
- 方法$1$: 模拟,面向题意的编程,时间复杂度接近$O(n^2)$.
以$4$棵灌木为例(可发现只要先模拟从左到右一次,再模拟从右到左一次,最后模拟从左到右一次即可找到每棵灌木的最大高度):
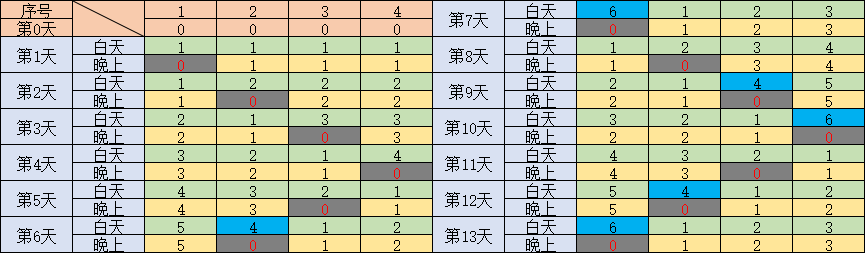

代码1
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 10010
using namespace std;
int n,a[MAXN],res[MAXN];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)//从左往右模拟一次
{
for(int j=1;j<=n;j++)
{
a[j]++;
res[j]=a[j]>res[j]?a[j]:res[j];
}//调用系统max会tle,原因不详,可能是时间复杂度为O(4 * n^2)
a[i]=0;
}
for(int i=n-1;i>=1;i--)//从右往左模拟一次
{
for(int j=1;j<=n;j++)
{
a[j]++;
res[j]=a[j]>res[j]?a[j]:res[j];
}
a[i]=0;
}
printf("%d\n",res[1]);
for(int i=2;i<=n;i++)//最后在从左往右枚举一次,并输出答案
{
for(int j=i;j<=n;j++)//此处是j=i
{
a[j]++;
res[j]=a[j]>res[j]?a[j]:res[j];
}
//a[i]=0;
printf("%d\n",res[i]);
}
return 0;
}
- 方法$2$: 找规律,我们可在方法$1$的模拟基础上发现左右的值刚好关于中心对称.
对于第$i(1 \leqslant i \leqslant n)$棵灌木进行分析:
- 当爱丽丝刚修剪过第$i$棵灌木且向右修剪直到尽头再左转要修剪到第$i$棵灌木的高度为$2 \times (n-i)$;
- 当爱丽丝刚修剪过第$i$棵灌木且向左修剪直到尽头再右转要修剪到第$i$棵灌木的高度为$2 \times (i-1)$;
故第$i$棵灌木最高高度为$2 \times max(n-i,i-1)$.
代码2
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 10010
using namespace std;
int n;
int main()
{
cin >> n;
for(int i=1;i<=n;i++)//或者i跑到(n+1)/2,并对称存储n+1-i的值
cout << 2*max(n-i,i-1) << endl;
return 0;
}
//另一种写法
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 10010
using namespace std;
int n,a[MAXN];
int main()
{
cin >> n;
for(int i=1;i<=(n+1)/2;i++)
a[i]=a[n+1-i]=2*max(n-i,i-1);
for(int i=1;i<=n;i++)
cout << a[i] << endl;
return 0;
}
试题 E: X 进制减法(15分)
问题描述
- 进制规定了数字在数位上逢几进一.
- $X$进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种$X$进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则$X$进制数$321$转换为十进制数为$65$.
- 现在有两个$X$进制表示的整数$A$和$B$,但是其具体每一数位的进制还不确定,只知道$A$和$B$是同一进制规则,且每一数位最高为$N$进制,最低为二进制.请你算出$A-B$的结果最小可能是多少.
- 请注意,你需要保证$A$和$B$在$X$进制下都是合法的,即每一数位上的数字要小于其进制.
输入格式
第一行一个正整数$N$,含义如题面所述.
第二行一个正整数$M_a$,表示$X$进制数$A$的位数.
第三行$M_a$个用空格分开的整数,表示$X$进制数$A$按从高位到低位顺序各个数位上的数字在十进制下的表示.
第四行一个正整数$M_b$,表示$X$进制数$B$的位数.
第五行$M_b$个用空格分开的整数,表示$X$进制数$B$按从高位到低位顺序各个数位上的数字在十进制下的表示.
请注意,输入中的所有数字都是十进制的.
输出格式
输出一行一个整数,表示$X$进制数$A-B$的结果的最小可能值转换为十进制后再模$1000000007$的结果.
样例输入
$11$
$3$
$10$ $4$ $0$
$3$
$1$ $2$ $0$样例输出
$94$
样例说明
当进制为:最低位$2$进制,第二数位$5$进制,第三数位$11$进制时,减法得到的差最小.此时$A$在十进制下是$108$,$B$在十进制下是$14$,差值是$94$.
评测用例规模与约定
- 对于$30$% 的评测用例,$N \leqslant 10$;$M_a,M_b \leqslant 8$.
- 对于$100$% 的评测用例,$2 \leqslant N \leqslant 1000$;$1 \leqslant M_a,M_b \leqslant 100000$;$A \geqslant B$.
思路
说实话这题我就没看懂这65是怎么得来的,就直接15分没了,所以看懂题是这题的关键之一.
先说说这$321$怎么转变为$65$(此处建议从右往左看).
| 百位 | 十位 | 个位 | |
|---|---|---|---|
| $X$进制数 | $3$ | $2$ | $1$ |
| $X$进制 | $8$ | $10$ | $2$ |
| 转化为$10$进制 | $3 \times 10 \times 2=60$ | $2 \times 2 =4$ | $1$ |
| 结果为$60+4+1=65$. |
推导过程:
设每一位的进制分别为为$P_{n-1},P_{n-2},…,P_1,P_0$,设$A$的进制数分别为$A_{n-1},A{n-2},…,A_1,A_0$,$B$的进制数分别为$B_{n-1},B_{n-2},…,B_1,B_0$($B$的位数可能小于$A$的位数,不足时前补$0$).
$A$用公式表示为:
$A=A_{n-1} \times \prod_{i=0}^{n-2}P_i + A_{n-2} \times \prod_{i=0}^{n-3}P_i +… + A_1 \times P_0+A_0$,
同理$B$也可用公式表示为:
$B=B_{n-1} \times \prod_{i=0}^{n-2}P_i + B_{n-2} \times \prod_{i=0}^{n-3}P_i +… + B_1 \times P_0+B_0$,
设$D=A-B$,每一位的差$D_i$为$A_i-B_i$,故
$D=(A_{n-1}-B_{n-1}) \times \prod_{i=0}^{n-2} P_i+ (A_{n-2}-B_{n-2}) \times \prod_{i=0}^{n-3} P_i + … + (A_1-B_1) \times P_0 + $
$(A_0-B_0)=D_{n-1} \times \prod_{i=0}^{n-2} P_i+ D_{n-2} \times \prod_{i=0}^{n-3} P_i + … + D_1 \times P_0 + D_0 \geqslant 0$.
将$P_k \times P_{k-1} \times P_{k-2} \times … \times P_0$(或$\prod_{i=0}^{k}P_i$)作为公因子提出,故可得到:
$D=(D_{n-1} \times \prod_{i=k+1}^{n-2}P_i+D_{n-2} \times \prod_{i=k+1}^{n-3}+… +D_{k+1}) \times \prod_{i=0}^{k}P_i$.
$(D_{n-1} \times \prod_{i=k+1}^{n-2}P_i+D_{n-2} \times \prod_{i=k+1}^{n-3}+… +D_{k+1})$表示的含义为在$k$左边$A$的前缀与$B$的前缀差,由于$A \geqslant B$,故$A$的前缀与$B$的前缀差也为非负数.故当前的$P_k$取值为$max(2,A_k+1,B_k+1)$.
最后怎么表示结果呢,借助秦九韶算法.
$f(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0$
$=(…((a_nx+a_{n-1})x+a_{n-2})x+…+a_1)x+a_0$.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 100010
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n,ma,mb;
int a[MAXN],b[MAXN];
int main()
{
cin >> n;
cin >> ma;
for(int i=ma-1;i>=0;i--)
cin >> a[i];
cin >> mb;
for(int i=mb-1;i>=0;i--)
cin >> b[i];
int res=0;
for(int i=ma-1;i>=0;i--)
res=(res*(ll)max({2,a[i]+1,b[i]+1})+a[i]-b[i])%mod;
cout << res << endl;
return 0;
}
试题 F: 统计子矩阵(15分)
问题描述
给定一个$N \times M$的矩阵$A$,请你统计有多少个子矩阵 (最小$1 \times 1$,最大$N × M$) 满足子矩阵中所有数的和不超过给定的整数$K$?
输入格式
- 第一行包含三个整数$N$,$M$和$K$.
- 之后$N$行每行包含$M$个整数,代表矩阵$A$.
输出格式
一个整数代表答案.
样例输入
$3$ $4$ $10$
$1$ $2$ $3$ $4$
$5$ $6$ $7$ $8$
$9$ $10$ $11$ $12$
样例输出
$19$样例说明
满足条件的子矩阵一共有$19$,包含:
- 大小为$1 \times 1$的有$10$个;
- 大小为$1 \times 2$的有$3$个;
- 大小为$1 \times 3$的有$2$个;
- 大小为$1 \times 4$的有$1$个;
- 大小为$2 \times 1$的有$3$个.
评测用例规模与约定
- 对于$30$% 的评测用例,$N,M \leqslant 20$.
- 对于$70$% 的评测用例,$N,M \leqslant 100$.
- 对于$100$% 的评测用例,$1 \leqslant N,M \leqslant 500;0 \leqslant A_{i j} \leqslant 1000; 1 \leqslant K \leqslant 250000000$.
思路
前缀和+双指针 ,时间复杂度为${\color{Blue} {O(n^3)}}$,
我虽然用到了二维前缀和,即枚举两个顶点的位置($4$重循环,时间复杂度为$O(n^4)$),结果肯定是t了,真不知道拿什么东西去优化
将矩阵中的元素转化为列前缀和,枚举上边界$i$和下边界$j$,把这每一小块构成一维数组,借助双指针枚举左边界$l$和右边界$r$,判断当前区间的值是否满足小于等于$K$,如果不满足则将左边界往右移直至满足条件,此时结果应加上$r-l+1$.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 510
using namespace std;
typedef long long ll;
int n,m,k;
int a[MAXN][MAXN];
int main()
{
scanf("%d %d %d",&n,&m,&k);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
a[i][j]+=a[i-1][j];
}
ll res=0;
for(int i=1;i<=n;i++)//枚举上边界
for(int j=i;j<=n;j++)//枚举下边界
{
int sum=0;
for(int l=1,r=1;r<=m;r++)
{
sum+=a[j][r]-a[i-1][r];
while(sum>k)
{
sum-=a[j][l]-a[i-1][l];
l++;
}
res+=r-l+1;
}
}
printf("%lld\n",res);
return 0;
}



