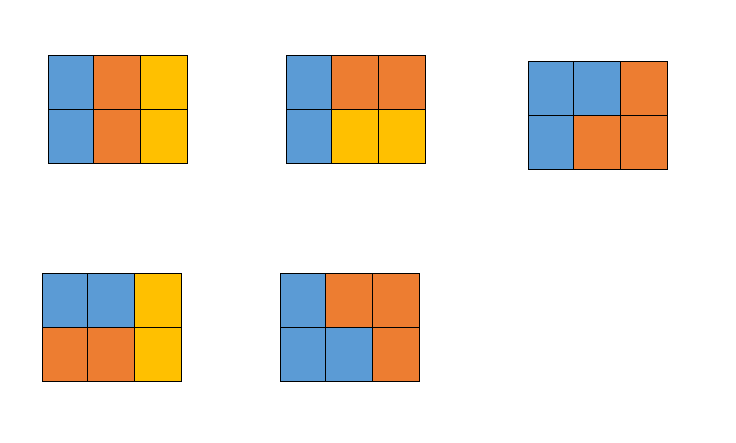试题 G: 积木画(20分)
问题描述
小明最近迷上了积木画,有这么两种类型的积木,分别为$I$型(大小为$2$个单位面积)和$L$型(大小为$3$个单位面积):
同时,小明有一块面积大小为$2 \times N$的画布,画布由$2 \times N$个$1 \times 1$区域构成.小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式?积木可以任意旋转,且画布的方向固定.
输入格式
输入一个整数$N$,表示画布大小.
输出格式
输出一个整数表示答案.由于答案可能很大,所以输出其对$1000000007$取模后的值.
样例输入
$3$
样例输出
$5$
样例说明
五种情况如下图所示,颜色只是为了标识不同的积木:
评测用例规模与约定
对于所有测试用例,$1 \leqslant N \leqslant 10000000$.
思路
分类讨论+dp思想,递推,设$dp[i]$为形成$i$列的方案数.
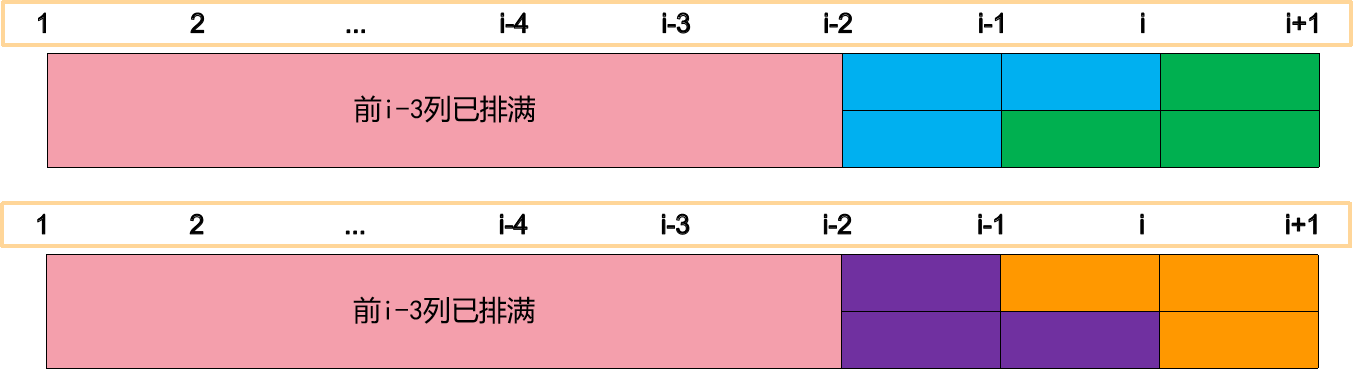
- 前$i-1$已经排满,此时的方案数为$dp[i-1]$,如下图所示;
- 第$i-1$列没排与第$i$列组合(前$i-2$列已经排满),此时的方案数为$dp[i-2]$,如下图所示;
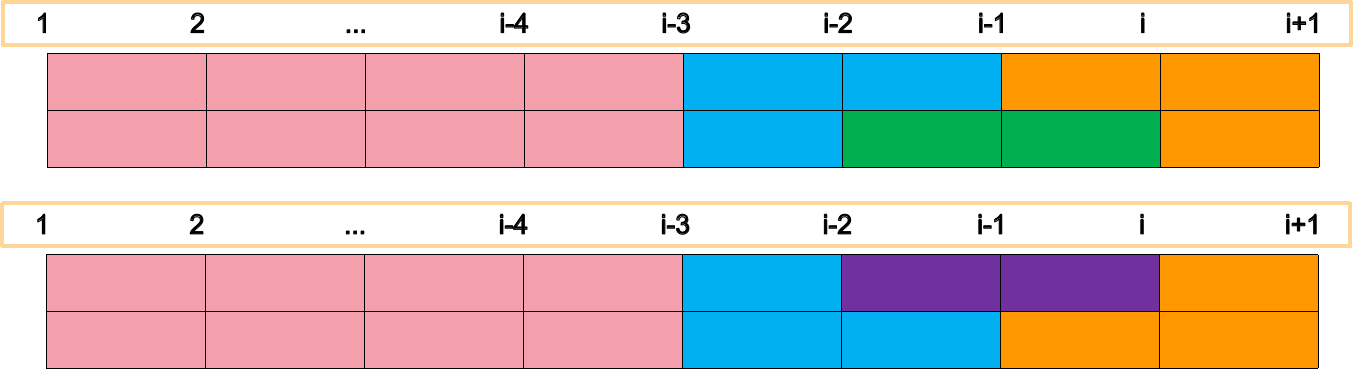
- 第$i-1$列排了一半(包括上半和下半)与第$i$列组合(两种小情况都是在满足前$i-3$列已经排满),此时的方案数为$2 \times dp[i-3]$,如下图所示;
由于情况三分得不够细(未考虑$i-3$的状态).- $i-3$与$i-2$组合,$i-1$与$i$组合,这种情况包含于情况二中,故不用再计算,如下图所示;
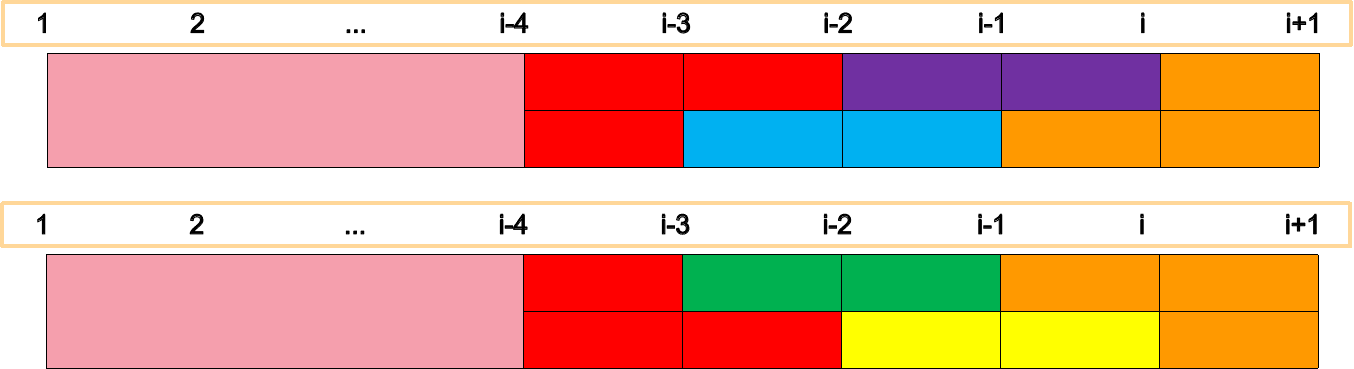
- 第$i-3$列与$i-2$形成正$’L’$,或倒$’L’$,此时的方案数为$2 \times dp[i-4]$;
同理,考虑$i-4$可得,方案数为$2 \times dp[i-5]$,如下图所示;
综上:$dp[i]=dp[i-1]+dp[i-2]+2 \times dp[i-3] +2 \times dp[i-4]+…+2 \times dp[2] +2 \times dp[1]$;
$dp[i-1]=dp[i-2]+dp[i-3]+2 \times dp[i-4] +2 \times dp[i-5]+…+2 \times dp[2] +2 \times dp[1]$;
两式作差:$dp[i]-dp[i-1]=dp[i-1]+dp[i-3]$;
最后化简得:$dp[i]=2 \times dp[i-1] +dp[i-3]$.
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 10000010
using namespace std;
typedef long long ll;
const int mod=1e9+7;
int n,dp[MAXN]={0,1,2,5};
int main()
{
cin >> n;
for(int i=4;i<=n;i++)
dp[i]=((ll)2*dp[i-1]+dp[i-3])%mod;
cout << dp[n] << endl;
return 0;
}
试题 H: 扫雷(20分)
问题描述
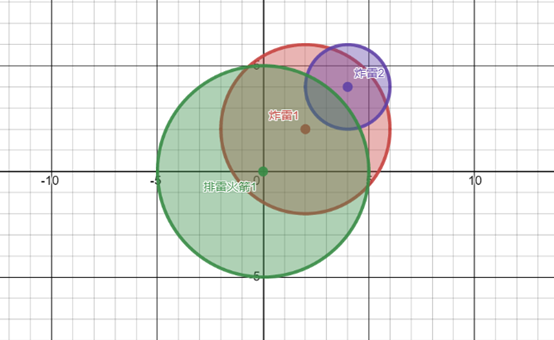
- 小明最近迷上了一款名为《扫雷》的游戏.其中有一个关卡的任务如下,在一个二维平面上放置着$n$个炸雷,第$i$个炸雷$(x_i,y_i,r_i)$表示在坐标$(x_i,y_i)$处存在一个炸雷,它的爆炸范围是以半径为$r_i$的一个圆.
- 为了顺利通过这片土地,需要玩家进行排雷.玩家可以发射$m$个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第$j$个排雷火箭$(x_j,y_j,r_j)$表示这个排雷火箭将会在$(x_j,y_j)$处爆炸,它的爆炸范围是以半径为$r_j$的一个圆,在其爆炸范围内的炸雷会被引爆.同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆.现在小明想知道他这次共引爆了几颗炸雷?
- 你可以把炸雷和排雷火箭都视为平面上的一个点.一个点处可以存在多个炸雷和排雷火箭.当炸雷位于爆炸范围的边界上时也会被引爆.
输入格式
- 输入的第一行包含两个整数$n、m$.
- 接下来的$n$行,每行三个整数$x_i,y_i,r_i$,表示一个炸雷的信息.
- 再接下来的$m$行,每行三个整数$x_j,y_j,r_j$,表示一个排雷火箭的信息.
输出格式
输出一个整数表示答案.
样例输入
$2$ $1$
$2$ $2$ $4$
$4$ $4$ $2$
$0$ $0$ $5$样例输出
$2$
样例说明
示例图如下,排雷火箭$1$覆盖了炸雷$1$,所以炸雷$1$被排除;炸雷$1$又覆盖了炸雷$2$,所以炸雷$2$也被排除.
评测用例规模与约定
- 对于$40$% 的评测用例,$0 \leqslant x,y \leqslant 10^9,0 \leqslant n,m \leqslant 10^3,1 \leqslant r \leqslant 10$.
- 对于$100$% 的评测用例,$0 \leqslant x,y \leqslant 10^9,0 \leqslant n,m \leqslant 5 \times 10^4,1 \leqslant r \leqslant 10$.
思路
该题点的数量较多,半径大的雷可以炸到半径小的雷,而半径小的雷不一定能引爆半径大的雷,故不能使用并查集解决(并查集一般用于无向图),故此处需用到图的遍历.
如果直接枚举每个雷和所有雷的情况,时间复杂度为$O(n^2)$,会$Tle$掉.
由于给定的$r \leqslant 10$,可直接对每个地雷周围一圈$r$进行遍历,时间复杂度为$O(n \times (2r)^2)$.
由于需要遍历每个坐标,需要通过坐标映射到雷的编号.
故需要考虑采用哈希,可采用如下三种方法:
- $map<pair<int,int>,int>$进行二维坐标点映射到雷的编号.
- 将$x,y$转化为字符串使用$unordered$_$map<string,int>$,即$to$ _ $string(x)+’\ ‘+to$ _ $string(y)$.
然而这两种方法容易被卡常$G$掉.
故只能通过手写哈希的方法实现.
- 通过$x,y$二维坐标唯一映射的哈希值:由于$x,y$的范围都是$0$~$1\times 10^9$,我们可以将x,y唯一的映射到一个哈希值,这个哈希值是一个$1\times 10^9+1$的进制数,即$x \times (10^9+1)+y$,可以类似的把$x,y$合起来看成一个数字,第$0$位是$y$,第$1$位是$x$.
- 哈希表的长度:题目已知$n$是小于等于$5\times 10^4$的,哈希表至少是$2n$,但是应该尽可能的开大,这样就可以避免冲突的发生;同时,哈希表的长度为质数时最好,取一个$999997$.
- $h[M]$数组表示哈希表,下标为$key$,值为$value$;$id[M]$数组表示哈希表中的每个$key$对应的地雷编号是多少;$vis[N]$数组表示该地雷是否被访问过.
代码给出两种方法:dfs和bfs.
代码
//dfs版本
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 50010
#define MAXM 999997
using namespace std;
typedef long long ll;
int n,m;
struct node{
int x;
int y;
int r;
}s[MAXN];
ll hash_[MAXM];
int vis[MAXM],id[MAXM];
ll get_key(int x,int y)
{
return (ll)x*1000000001+y;
}
int find(int x,int y)
{
ll key=get_key(x,y);
int temp=(key%MAXM+MAXM)%MAXM;
while(hash_[temp]!=-1&&hash_[temp]!=key)
if(++temp==MAXM)
temp=0;
return temp;
}
int sqr(int n)
{
return n*n;
}
void dfs(int x,int y,int r)
{
vis[find(x,y)]=1;
for(int i=x-r;i<=x+r;i++)
for(int j=y-r;j<=y+r;j++)
if(sqr(i-x)+sqr(j-y)<=sqr(r))
{
int temp=find(i,j);
if(id[temp]&&vis[temp]==0)
dfs(i,j,s[id[temp]].r);
}
}
int main()
{
memset(hash_,-1,sizeof(hash_));
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
int x,y,r;
scanf("%d %d %d",&x,&y,&r);
s[i]={x,y,r};
int temp=find(x,y);
if(hash_[temp]==-1)
hash_[temp]=get_key(x,y);
if(id[temp]==0||s[id[temp]].r<r)
id[temp]=i;
}
while(m--)
{
int x,y,r;
scanf("%d %d %d",&x,&y,&r);
for(int i=x-r;i<=x+r;i++)
for(int j=y-r;j<=y+r;j++)
if(sqr(i-x)+sqr(j-y)<=sqr(r))
{
int temp=find(i,j);
if(id[temp]&&vis[temp]==0)
dfs(i,j,s[id[temp]].r);
}
}
int res=0;
for(int i=1;i<=n;i++)
if(vis[find(s[i].x,s[i].y)])
res++;
printf("%d\n",res);
return 0;
}
//bfs版本
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define MAXN 50010
#define MAXM 999997
using namespace std;
typedef long long ll;
int n,m;
struct node{
int x;
int y;
int r;
}s[MAXN];
ll hash_[MAXM];
int vis[MAXM],id[MAXM];
ll get_key(int x,int y)
{
return (ll)x*1000000001+y;
}
int find(int x,int y)
{
ll key=get_key(x,y);
int temp=(key%MAXM+MAXM)%MAXM;
while(hash_[temp]!=-1&&hash_[temp]!=key)
if(++temp==MAXM)
temp=0;
return temp;
}
int sqr(int n)
{
return n*n;
}
void bfs(int pos)
{
queue<int> q;
q.push(id[pos]);
vis[pos]=1;
while(q.size()>0)
{
int temp=q.front();
q.pop();
for(int i=s[temp].x-s[temp].r;i<=s[temp].x+s[temp].r;i++)
for(int j=s[temp].y-s[temp].r;j<=s[temp].y+s[temp].r;j++)
if(sqr(i-s[temp].x)+sqr(j-s[temp].y)<=sqr(s[temp].r))
{
int temp_=find(i,j);
if(id[temp_]&&vis[temp_]==0)
{
q.push(id[temp_]);
vis[temp_]=1;
}
}
}
}
int main()
{
memset(hash_,-1,sizeof(hash_));
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
int x,y,r;
scanf("%d %d %d",&x,&y,&r);
s[i]={x,y,r};
int temp=find(x,y);
if(hash_[temp]==-1)
hash_[temp]=get_key(x,y);
if(id[temp]==0||s[id[temp]].r<r)
id[temp]=i;
}
while(m--)
{
int x,y,r;
scanf("%d %d %d",&x,&y,&r);
for(int i=x-r;i<=x+r;i++)
for(int j=y-r;j<=y+r;j++)
if(sqr(i-x)+sqr(j-y)<=sqr(r))
{
int temp=find(i,j);
if(id[temp]&&vis[temp]==0)
bfs(temp);
}
}
int res=0;
for(int i=1;i<=n;i++)
if(vis[find(s[i].x,s[i].y)])
res++;
printf("%d\n",res);
return 0;
}
试题 I: 李白打酒加强版(25分)
问题描述
- 话说大诗人李白,一生好饮.幸好他从不开车.
- 一天,他提着酒壶,从家里出来,酒壶中有酒$2$斗.他边走边唱:
无事街上走,提壶去打酒.
逢店加一倍,遇花喝一斗. - 这一路上,他一共遇到店$N$次,遇到花$M$次.已知最后一次遇到的是花,他正好把酒喝光了.
- 请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
- 注意:壶里没酒($0$斗)时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的.
输入格式
第一行包含两个整数$N$和$M$.
输出格式
输出一个整数表示答案.由于答案可能很大,输出模$1000000007$的结果.
样例输入
$5$ $10$
样例输出
$14$
样例说明
如果我们用$0$代表遇到花,$1$代表遇到店,$14$种顺序如下:
$010101101000000$
$010110010010000$
$011000110010000$
$100010110010000$
$011001000110000$
$100011000110000$
$100100010110000$
$010110100000100$
$011001001000100$
$100011001000100$
$100100011000100$
$011010000010100$
$100100100010100$
$101000001010100$评测用例规模与约定
- 对于$40$% 的评测用例,$1 \leqslant n,m \leqslant 10$.
- 对于$100$% 的评测用例,$1 \leqslant n,m \leqslant 100$.
思路
dp.
设$dp(i,j,k)$表示当前经过$i$个店,经过$j$朵花且壶中酒的量为$k$的方案数.
- 考虑第$i$次经过的是店且酒的量为$k$,它是由$i-1$次遇到店且酒的量为$\frac{k}{2}$转移而来,即 $dp[i][j][k]=dp[i-1][j][\frac{k}{2}]$,还需满足$k$为偶数,并且$i-1\geqslant 0$;
- 考虑第$j$次经过的是花且酒的量为$k$,它是由$j-1$次遇到花且酒的量为$k+1$转移而来,即$dp[i][j][k]=dp[i][j-1][k+1]$,同理还需满足$j-1 \geqslant 0$.
初始化$dp[0][0][2]=1$,结果应为$dp[n][m-1][1]$(需要满足最后一次遇到的是花,且壶中的酒为$0$).
代码
#include <iostream>
#include <cstring>
#include <algorithm>
#define MAXN 110
using namespace std;
const int mod=1e9+7;
int n,m;
int dp[MAXN][MAXN][MAXN];
int main()
{
cin >> n >> m;
dp[0][0][2]=1;
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++)
for(int k=0;k<=m;k++)
{
if(i>=1&&k%2==0)
dp[i][j][k]=(dp[i][j][k]+dp[i-1][j][k/2])%mod;
if(j>=1)
dp[i][j][k]=(dp[i][j][k]+dp[i][j-1][k+1])%mod;
}
cout << dp[n][m-1][1] << endl;
return 0;
}
试题 J: 砍竹子(25分)
问题描述
- 这天,小明在砍竹子,他面前有$n$棵竹子排成一排,一开始第$i$棵竹子的高度为$h_i$.
- 他觉得一棵一棵砍太慢了,决定使用魔法来砍竹子.魔法可以对连续的一段相同高度的竹子使用,假设这一段竹子的高度为$H$,那么使用一次魔法可以把这一段竹子的高度都变为$\left \lfloor \sqrt{\left \lfloor \frac{H}{2} \right \rfloor +1} \right \rfloor$,其中$\left \lfloor x\right \rfloor$表示对$x$向下取整.小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为$1$.
输入格式
- 第一行为一个正整数$n$表示竹子的棵数.
- 第二行共$n$个空格分开的正整数$h_i$,表示每棵竹子的高度.
输出格式
一个整数表示答案.
样例输入
$6$
$2$ $1$ $4$ $2$ $6$ $7$样例输出
$5$
样例说明
其中一种方案:$2$ $1$ $4$ $2$ $6$ $7$
$\rightarrow$ $2$ $1$ $4$ $2$ $6$ $2$
$\rightarrow$ $2$ $1$ $4$ $2$ $2$ $2$
$\rightarrow$ $2$ $1$ $1$ $2$ $2$ $2$
$\rightarrow$ $1$ $1$ $1$ $2$ $2$ $2$
$\rightarrow$ $1$ $1$ $1$ $1$ $1$ $1$
共需要5步完成评测用例规模与约定
- 对于$20$% 的评测用例,$n \leqslant 1000,h_i \leqslant 10^6$.
- 对于$100$% 的评测用例,$n \leqslant 2 \times 10^5,h_i \leqslant 10^{18}$.
思路
方法一:贪心+优先队列.优先枚举较大的区间并进行合并,我是想到了,我好像用成$cout$而且忘写$return$ $0$了,关键难题对了又没完全对,有时候能对,时间复杂度为$O(6nlogn)$.
方法二:贪心,将每一个数进行操作的结果存在数组中(由于$10^{18}$只需要进行6次操作就可以变成1)并且结果加上操作的次数,最后只需要枚举每一层是否存在相邻的数,存在结果$-1$,时间复杂度为$O(6n)$.
代码
//优先队列法
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#define MAXN 200010
using namespace std;
typedef long long ll;
typedef pair<ll,int> PII;
int n,cnt;
ll a[MAXN];
priority_queue<PII> q;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
q.push({a[i],i});
}
while(q.size()>0)
{
if(q.top().first==1)
break;
PII temp=q.top();
//cout << temp.first << " " << temp.second << endl;
q.pop();
q.push({(ll)sqrt(temp.first/2+1),temp.second});
while(q.top().first==temp.first&&q.top().second==temp.second-1)
{
q.push({(ll)sqrt(temp.first/2+1),q.top().second});
temp.second--;
q.pop();
}
cnt++;
}
printf("%d\n",cnt);
return 0;
}
//贪心
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
#include <cmath>
#define MAXN 200010
#define MAXM 10
using namespace std;
typedef long long ll;
int n,m;
ll f[MAXN][MAXM];
int main()
{
scanf("%d",&n);
stack<ll> sta;
int res=0;
for(int i=1;i<=n;i++)
{
ll x;
scanf("%lld",&x);
int cnt=0;
while(x>1)
{
sta.push(x);
x=sqrt(x/2+1);
cnt++;
}
res+=cnt;
m=max(m,cnt);
int j=0;
while(sta.size()>0)
{
f[i][++j]=sta.top();
sta.pop();
}
}
for(int i=1;i<=m;i++)
for(int j=2;j<=n;j++)
if(f[j][i]&&f[j][i]==f[j-1][i])
res--;
printf("%d\n",res);
return 0;
}